Curiosidades Museo de Ciencia y Técnica [fui y t

El Museo de Ciencia y Técnica de Bahía Blanca es una SOCIEDAD CIVIL sin fines de lucro destinada a poner al alcance de grupos escolares y público en general la posibilidad de ver e interactuar con experimentos que facilitan el aprendizaje de varias disciplinas.



En este post y los que le sigan porque el recorrido es largo y las curiosidades son muchas, quiero compartir con ustedes una recorrida por sus instalaciones. Son fotos tomadas por mi con recopilación de información y apuntes tomados en la propia visita. Si algún día tienen la posibilidad de visitarlo, se los recomiendo, les permitirá conocer temas referidos a matemática, física y otras ciencias interactuando con las exposiciones de la muestra, un gran trabajo de puesta en escena y orientación. El valor de la entrada es de $18. El museo se encuentra en la calle Zelarrayán 2528 (Bahía Blanca)



EL HOMBRE DE VITRUVIO (DA VINCI)

El Hombre de Vitruvio es un famoso dibujo acompañado de notas anatómicas de Leonardo da Vinci realizado alrededor del año 1487 en uno de sus diarios. Representa una figura masculina desnuda en dos posiciones sobreimpresas de brazos y piernas e inscrita en un círculo y un cuadrado. Se trata de un estudio de las proporciones del cuerpo humano, realizado a partir de los textos de arquitectura de Vitruvio, arquitecto de la antigua Roma, del cual el dibujo toma su nombre.

De acuerdo con las notas del propio Leonardo en el Hombre de Vitruvio se dan otras relaciones:

* Una palma equivale al ancho de cuatro dedos.
* Un pie equivale al ancho de cuatro palmas (12 pulgadas).
* Un antebrazo equivale al ancho de seis palmas.
* La altura de un hombre son cuatro antebrazos (24 palmas).
* Un paso es igual a un antebrazo.
* La longitud de los brazos extendidos (envergadura) de un hombre es igual a su altura.
* La distancia entre el nacimiento del pelo y la barbilla es un décimo de la altura de un hombre.
* La altura de la cabeza hasta la barbilla es un octavo de la altura de un hombre.
* La distancia entre el nacimiento del pelo a la parte superior del pecho es un séptimo de la altura de un hombre.
* La altura de la cabeza hasta el final de las costillas es un cuarto de la altura de un hombre.
* La anchura máxima de los hombros es un cuarto de la altura de un hombre.
* La distancia del codo al extremo de la mano es un quinto de la altura de un hombre.
* La distancia del codo a la axila es un octavo de la altura de un hombre.
* La longitud de la mano es un décimo de la altura de un hombre.
* La distancia de la barbilla a la nariz es un tercio de la longitud de la cara.
* La distancia entre el nacimiento del pelo y las cejas es un tercio de la longitud de la cara.
* La altura de la oreja es un tercio de la longitud de la cara.
* La distancia desde la planta del pie hasta debajo de la rodilla es la cuarta parte del hombre.
* La distancia desde debajo de la rodilla hasta el inicio de los genitales es la cuarta parte del hombre.
* El inicio de los genitales marca la mitad de la altura del hombre.

El redescubrimiento de las proporciones matemáticas del cuerpo humano en el siglo XV por Leonardo y otros autores, está considerado como uno de los grandes logros del Renacimiento.

El dibujo también es a menudo considerado como un símbolo de la simetría básica del cuerpo humano y, por extensión, del universo en su conjunto.



LAS TORRES DE HANOI


LAS TORRES DE HANOI es un clásico de los juegos de estrategia inventado en 1883 por el matemático francés Éduard Lucas. Se parte de tres niveles, en el primero de las cuales hay n discos de diámetros diferentes formando una torre. Se trata de llevar los n discos al tercer nivel, conservando la forma de torre.

Para realizar este objetivo, es necesario seguir tres simples reglas:

1. Sólo se puede mover un disco cada vez.
2. Un disco de mayor tamaño no puede descansar sobre uno más pequeño que él mismo.
3. Sólo puedes desplazar el disco que se encuentre arriba en cada varilla.

Existen diversas formas de realizar la solución final, todas ellas siguiendo estrategias diversas.

El número de movimientos mínimo a realizar para resolver el problema es de (2^n)-1, siendo n el número de fichas.

El problema de las Torres de Hanói es muy curioso porque su solución es muy rápida de calcular, pero el número de pasos para resolverlo crece exponencialmente conforme aumenta el número de discos.

A la hora de resolver matemáticamente el problema, nos encontramos con muchas curiosidades matemáticas respecto a la resolución. Son las siguientes:

- La ficha número n (siendo 1 la más pequeña) se mueve por primera vez en el paso número 2^(n-1), y después de ese primer movimiento, se moverá cada 2^n movimientos. De este modo, la ficha 1, se mueve en 1, 3, 5, 7, 9... etc. La ficha 3, se mueve en 4, 12, 20, 28, 32... etc
- Todas las fichas impares (siendo 1 la más pequeña) se mueven siguiendo el mismo patrón. Asimismo, todas las fichas pares se mueven siguiendo el patrón inverso a las impares. Por ejemplo: si queremos mover un número impar de piezas desde la columna 1 hasta la 3, sucederá lo siguiente:
- Todas las fichas impares seguirán este patrón de movimiento: 1 -> 3 -> 2 -> 1 -> 3 -> 2 -> 1 -> 3 -> 2 -> 1.
- Todas las fichas pares seguirán este patrón de movimiento: 1 -> 2 -> 3 -> 1 -> 2 -> 3 -> 1 -> 2 -> 3

Estos patrones dependen únicamente del número de piezas. Si el número de piezas es par, los patrones de las impares serán los de las pares, y viceversa.

- Uniendo la primera regla con la segunda, sabemos siempre qué pieza hay que mover y a qué columna hay que desplazarla, luego el problema está resuelto.



JUGALO!




link: http://www.publijuegos.com/flash/hanoi.swf




CURVA CICLOIDE



Si tenemos dos puntos A y B, a diferente altura, ¿cuál es la forma más rápida de conectarlos? Es decir, si los unimos mediante una rampa y tiramos por ella una pelotita, ¿que forma debe tener para que tarde el menor tiempo posible en bajar por su propio peso?

Una primera respuesta intuitiva es que la rampa sea una línea recta:



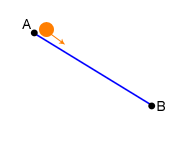
Sin embargo, nada más lejos de la realidad. Aunque la línea recta es la distancia más corta entre dos puntos, no es la más rápida.

La cicloide es la curva que genera un punto de una circunferencia que rueda sobre una línea recta, es decir, lo que dibujaría un rotulador pegado a la rueda de tu bicicleta, mientras te das un paseo pegado a la pared.



Incluso si los puntos A y B están situados de manera que haya que bajar para luego volver a subir, la cicloide invertida será el camino más corto. Por eso se la llama también braquistócrona (del grigo ?más corto? y ?tiempo?).



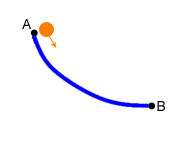
El problema de la braquistócrona fue propuesto por el matemático suizo Johann Bernoulli en 1696, que lanzó el desafío al resto de la comunidad matemática. Sólo cinco personas supieron responder correstamente: él mismo, Gottfried Leibniz, el Marqués de L?Hôpital, y otros dos que a buen seguro no agradaron a Johann. Uno de ellos fue su hermano Jakob y otro el gran Isaac Newton, con quien Johann no se llevaba nada bien debido a la disputa que mantenía con Leibniz acerca de la creación de esa herramienta tan útil hoy día: el cálculo. ¿Te suenan?

Pero la cicloide tiene más propiedades interesantes. Huygens descubrió que, además de braquistócrona, es tautócrona. Es decir, si volvemos a nuestro tobogán con forma de cicloide invertida, y lanzamos ahora dos pelotas, éstas llegan al mismo tiempo al punto más bajo de la cicloide (despreciando el rozamiento).



MÁQUINA DE GALTON





En la Máquina de Galton se lanzan bolas en una red de clavos. Cada vez que una bola choca con un clavo tiene una probabilidad del 50 % de caer tanto a la izquierda como a la derecha. Al acumularse en las celdas situadas bajo la red de clavos las bolas parecen dibujar una curva de distribución normal o binómica. La famosa Curva de Gauss!!

ACA ESTOY YO SACANDO LA FOTO! (gracias profe)





EL INVENTOR DEL AJEDREZ



Una leyenda cuenta que el inventor del ajedrez presentó su invento al Rey de Persia. El príncipe quedó tan impresionado que quiso premiarle generosamente, y le dijo: «Pídeme lo que quieras, que te lo daré». El inventor del ajedrez formuló su petición del modo siguiente: «Deseo que me entregues un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta, dieciséis por la quinta, y así sucesivamente hasta la casilla 64». Cuando el príncipe calculó la cantidad de trigo que representaba la petición del inventor, vio que toda la Tierra sembrada de trigo era insuficiente para obtener lo que éste pedía. Utilizando la calculadora podemos hallar el total de granos de trigo: 1 + 2 + 22 + 23 + ... + 262 + 263

Se necesitaría la cantidad de:

264 granos de trigo = 18,446,744,073,709,551,616 granos

Diez y ocho trillones, cuatrocientos cuarenta y seis mil setecientos cuarenta y cuatro billones, setenta y tres mil setecientos nueve millones, quinientos cincuenta y un mil seiscientos dieciséis granos de trigo.

En cada kilogramo de trigo caben aproximadamente unos 28,220 granos, por lo que el resultado sería de unas 653,676,260,585 toneladas; que ocuparían un depósito en forma de cubo de algo más de 11.5 kilómetros de lado.

Para producir tal cantidad de trigo se necesitaría estar cultivando la Tierra (incluidos los mares), durante ocho años!!!






En El o Los Próximos Posts:

* Diablillo de Descartes
* Giroscopio. PRUEBA PROPIA ( ACA ESTOY YO )



* Eje de giro ( TAMBIEN ME SUBI )



* Palanca, polea y aparejo. AHI ESTOY YO OTRA VEZ..



* Efecto Coriolis
* El Péndulo que dibuja
* El Theremin..... Y MUCHO MÁS



PARA IR A LA SEGUNDA PARTE DEL POST:

http://www./posts/ciencia-educacion/10554116/Curiosidades-Museo-de-Ciencia-y-Tecnica-_parte-2_.html








link: http://www.youtube.com/watch?v=FNjUl2fx5YU




No olvides visitar de nuevo Curiosidades Museo de Ciencia y Técnica [fui y t